The Pythagorean Theorem states that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. Mathematically, for a triangle with sides of lengths a, b (the legs), and c (the hypotenuse), the formula is: a² + b² = c².
This theorem, attributed to the ancient Greek mathematician Pythagoras (around 570–495 BCE), forms a cornerstone of Euclidean geometry and is essential for solving problems involving distances, such as in coordinate geometry, trigonometry, and physics.
Applications include calculating distances in navigation, engineering designs, computer graphics, and even in fields like architecture and astronomy. For example, it helps determine the length of a ladder needed to reach a certain height on a wall.
To prove it, one common method is using similar triangles or rearranging geometric shapes, but it can also be derived algebraically. Its simplicity and universality make it a fundamental concept in mathematics education worldwide.
Table of contents
- Part 1: Create an amazing pythagorean theorem quiz using AI instantly in OnlineExamMaker
- Part 2: 20 pythagorean theorem quiz questions & answers
- Part 3: OnlineExamMaker AI Question Generator: Generate questions for any topic
Part 1: Create an amazing pythagorean theorem quiz using AI instantly in OnlineExamMaker
The quickest way to assess the pythagorean theorem knowledge of candidates is using an AI assessment platform like OnlineExamMaker. With OnlineExamMaker AI Question Generator, you are able to input content—like text, documents, or topics—and then automatically generate questions in various formats (multiple-choice, true/false, short answer). Its AI Exam Grader can automatically grade the exam and generate insightful reports after your candidate submit the assessment.
Overview of its key assessment-related features:
● Create up to 10 question types, including multiple-choice, true/false, fill-in-the-blank, matching, short answer, and essay questions.
● Automatically generates detailed reports—individual scores, question report, and group performance.
● Instantly scores objective questions and subjective answers use rubric-based scoring for consistency.
● API and SSO help trainers integrate OnlineExamMaker with Google Classroom, Microsoft Teams, CRM and more.
Automatically generate questions using AI
Part 2: 20 pythagorean theorem quiz questions & answers
or
Question 1:
In a right-angled triangle, the lengths of the two legs are 3 cm and 4 cm. What is the length of the hypotenuse?
A) 5 cm
B) 6 cm
C) 7 cm
D) 8 cm
Answer: A) 5 cm
Explanation: Using the Pythagorean theorem, c = √(3² + 4²) = √(9 + 16) = √25 = 5 cm.
Question 2:
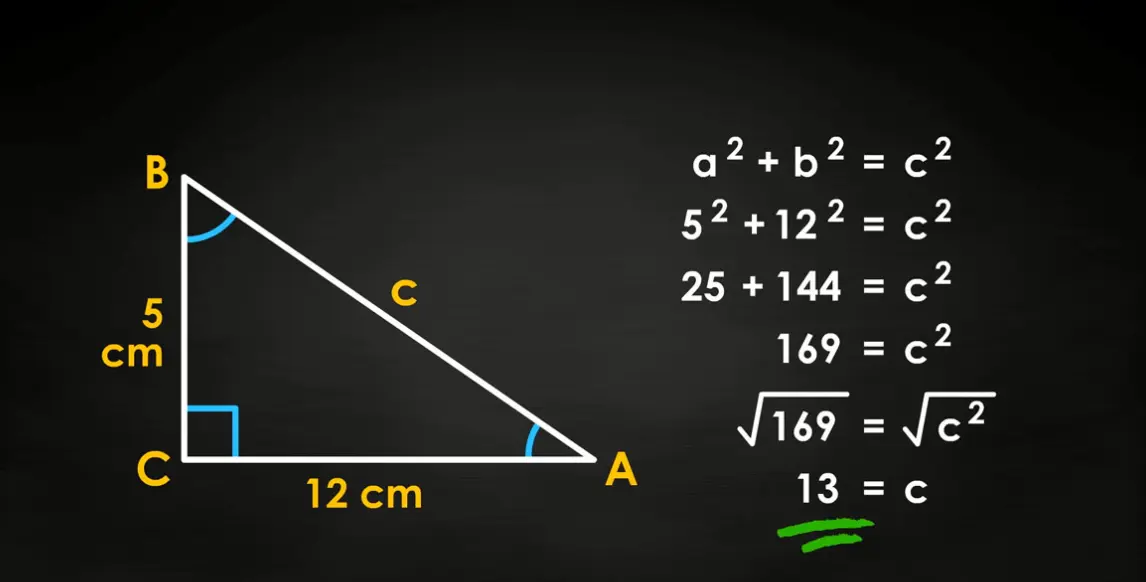
A ladder is leaning against a wall. The base of the ladder is 5 meters from the wall, and the ladder reaches 12 meters up the wall. How long is the ladder?
A) 13 meters
B) 14 meters
C) 15 meters
D) 16 meters
Answer: A) 13 meters
Explanation: Applying the Pythagorean theorem, ladder length c = √(5² + 12²) = √(25 + 144) = √169 = 13 meters.
Question 3:
In a right-angled triangle, one leg is 6 cm, and the hypotenuse is 10 cm. What is the length of the other leg?
A) 8 cm
B) 7 cm
C) 9 cm
D) 6 cm
Answer: A) 8 cm
Explanation: Using the Pythagorean theorem, b = √(c² – a²) = √(10² – 6²) = √(100 – 36) = √64 = 8 cm.
Question 4:
The sides of a right-angled triangle are 5 cm, 12 cm, and x cm, where x is the hypotenuse. What is x?
A) 13 cm
B) 14 cm
C) 15 cm
D) 16 cm
Answer: A) 13 cm
Explanation: By the Pythagorean theorem, x = √(5² + 12²) = √(25 + 144) = √169 = 13 cm.
Question 5:
A right-angled triangle has legs of 7 cm and 24 cm. What is the hypotenuse?
A) 25 cm
B) 26 cm
C) 27 cm
D) 28 cm
Answer: A) 25 cm
Explanation: Using the Pythagorean theorem, c = √(7² + 24²) = √(49 + 576) = √625 = 25 cm.
Question 6:
One leg of a right-angled triangle is 8 cm, and the hypotenuse is 17 cm. Find the other leg.
A) 15 cm
B) 14 cm
C) 16 cm
D) 13 cm
Answer: A) 15 cm
Explanation: Applying the Pythagorean theorem, b = √(17² – 8²) = √(289 – 64) = √225 = 15 cm.
Question 7:
In a right-angled triangle, the legs are 9 cm and 12 cm. What is the length of the hypotenuse?
A) 15 cm
B) 16 cm
C) 17 cm
D) 18 cm
Answer: A) 15 cm
Explanation: The Pythagorean theorem gives c = √(9² + 12²) = √(81 + 144) = √225 = 15 cm.
Question 8:
A triangle has sides 10 cm, 24 cm, and a hypotenuse of 26 cm. Verify if it is a right-angled triangle.
A) Yes
B) No
Answer: A) Yes
Explanation: Check with the Pythagorean theorem: 10² + 24² = 100 + 576 = 676, and 26² = 676, so it is a right-angled triangle.
Question 9:
The hypotenuse of a right-angled triangle is 13 cm, and one leg is 5 cm. What is the other leg?
A) 12 cm
B) 11 cm
C) 10 cm
D) 9 cm
Answer: A) 12 cm
Explanation: Using the Pythagorean theorem, b = √(13² – 5²) = √(169 – 25) = √144 = 12 cm.
Question 10:
In a right-angled triangle, the sides are 11 cm and 60 cm as legs. What is the hypotenuse?
A) 61 cm
B) 62 cm
C) 63 cm
D) 64 cm
Answer: A) 61 cm
Explanation: The Pythagorean theorem states c = √(11² + 60²) = √(121 + 3600) = √3721 = 61 cm.
Question 11:
One leg is 15 cm, and the hypotenuse is 17 cm. Find the other leg.
A) 8 cm
B) 9 cm
C) 10 cm
D) 7 cm
Answer: A) 8 cm
Explanation: By the Pythagorean theorem, b = √(17² – 15²) = √(289 – 225) = √64 = 8 cm.
Question 12:
A right-angled triangle has legs of 20 cm and 21 cm. What is the hypotenuse?
A) 29 cm
B) 28 cm
C) 30 cm
D) 27 cm
Answer: A) 29 cm
Explanation: Using the Pythagorean theorem, c = √(20² + 21²) = √(400 + 441) = √841 = 29 cm.
Question 13:
In a right-angled triangle, one leg is 12 cm, and the hypotenuse is 37 cm. What is the other leg?
A) 35 cm
B) 36 cm
C) 34 cm
D) 33 cm
Answer: A) 35 cm
Explanation: The Pythagorean theorem gives b = √(37² – 12²) = √(1369 – 144) = √1225 = 35 cm.
Question 14:
The legs of a right-angled triangle are 13 cm and 84 cm. Find the hypotenuse.
A) 85 cm
B) 86 cm
C) 87 cm
D) 88 cm
Answer: A) 85 cm
Explanation: Applying the Pythagorean theorem, c = √(13² + 84²) = √(169 + 7056) = √7225 = 85 cm.
Question 15:
A hypotenuse is 25 cm, and one leg is 7 cm. What is the other leg?
A) 24 cm
B) 23 cm
C) 22 cm
D) 21 cm
Answer: A) 24 cm
Explanation: Using the Pythagorean theorem, b = √(25² – 7²) = √(625 – 49) = √576 = 24 cm.
Question 16:
In a right-angled triangle, the sides are 18 cm and 80 cm as legs. What is the hypotenuse?
A) 82 cm
B) 83 cm
C) 84 cm
D) 81 cm
Answer: A) 82 cm
Explanation: The Pythagorean theorem states c = √(18² + 80²) = √(324 + 6400) = √6724 = 82 cm.
Question 17:
One leg is 16 cm, and the hypotenuse is 20 cm. Find the other leg.
A) 12 cm
B) 13 cm
C) 14 cm
D) 11 cm
Answer: A) 12 cm
Explanation: By the Pythagorean theorem, b = √(20² – 16²) = √(400 – 256) = √144 = 12 cm.
Question 18:
A right-angled triangle has legs of 28 cm and 45 cm. What is the hypotenuse?
A) 53 cm
B) 54 cm
C) 55 cm
D) 52 cm
Answer: A) 53 cm
Explanation: Using the Pythagorean theorem, c = √(28² + 45²) = √(784 + 2025) = √2809 = 53 cm.
Question 19:
In a right-angled triangle, one leg is 9 cm, and the hypotenuse is 41 cm. What is the other leg?
A) 40 cm
B) 39 cm
C) 38 cm
D) 37 cm
Answer: A) 40 cm
Explanation: The Pythagorean theorem gives b = √(41² – 9²) = √(1681 – 81) = √1600 = 40 cm.
Question 20:
The legs of a right-angled triangle are 33 cm and 56 cm. Find the hypotenuse.
A) 65 cm
B) 66 cm
C) 67 cm
D) 64 cm
Answer: A) 65 cm
Explanation: Applying the Pythagorean theorem, c = √(33² + 56²) = √(1089 + 3136) = √4225 = 65 cm.
or
Part 3: OnlineExamMaker AI Question Generator: Generate questions for any topic
Automatically generate questions using AI