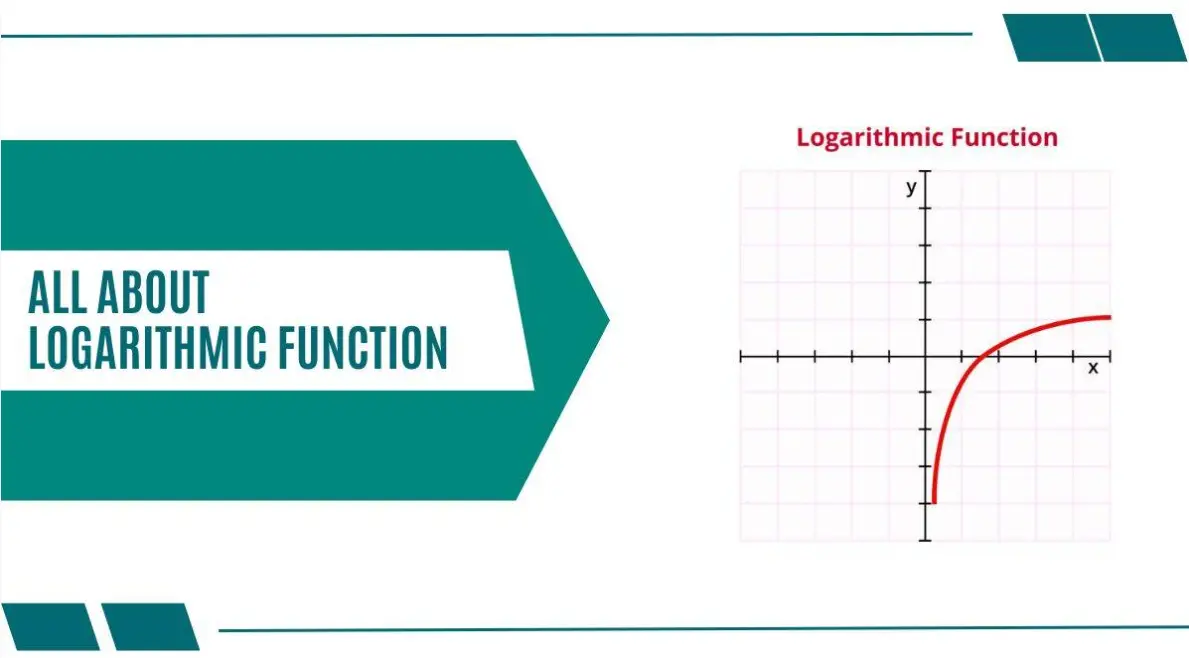
Logarithmic functions are mathematical functions that are the inverses of exponential functions. They are defined as y = log_b(x), where b is the base (a positive number not equal to 1), and x is a positive real number. The function represents the exponent to which the base b must be raised to obtain x.
Key properties include:
– The domain is x > 0, and the range is all real numbers.
– Basic values: log_b(1) = 0, log_b(b) = 1, and log_b(b^k) = k.
– Logarithm rules:
– Product rule: log_b(xy) = log_b(x) + log_b(y)
– Quotient rule: log_b(x/y) = log_b(x) – log_b(y)
– Power rule: log_b(x^k) = k * log_b(x)
– Change of base: log_b(x) = log_c(x) / log_c(b) for any positive c ≠ 1
Common types:
– Natural logarithm: ln(x) = log_e(x), where e ≈ 2.71828
– Common logarithm: log(x) or log_10(x), base 10
Graphs of logarithmic functions are increasing or decreasing curves depending on the base (b > 1 for increasing, 0 < b < 1 for decreasing). They pass through (1, 0) and have a vertical asymptote at x = 0.
Table of contents
- Part 1: Create an amazing logarithmic functions quiz using AI instantly in OnlineExamMaker
- Part 2: 20 logarithmic functions quiz questions & answers
- Part 3: AI Question Generator – Automatically create questions for your next assessment
Part 1: Create an amazing logarithmic functions quiz using AI instantly in OnlineExamMaker
The quickest way to assess the logarithmic functions knowledge of candidates is using an AI assessment platform like OnlineExamMaker. With OnlineExamMaker AI Question Generator, you are able to input content—like text, documents, or topics—and then automatically generate questions in various formats (multiple-choice, true/false, short answer). Its AI Exam Grader can automatically grade the exam and generate insightful reports after your candidate submit the assessment.
Overview of its key assessment-related features:
● Create up to 10 question types, including multiple-choice, true/false, fill-in-the-blank, matching, short answer, and essay questions.
● Automatically generates detailed reports—individual scores, question report, and group performance.
● Instantly scores objective questions and subjective answers use rubric-based scoring for consistency.
● API and SSO help trainers integrate OnlineExamMaker with Google Classroom, Microsoft Teams, CRM and more.
Automatically generate questions using AI
Part 2: 20 logarithmic functions quiz questions & answers
or
1. Question: What is the value of \(\log_2 8\)?
A) 1
B) 2
C) 3
D) 4
Answer: C) 3
Explanation: Since \(2^3 = 8\), \(\log_2 8 = 3\).
2. Question: Simplify \(\log(100)\).
A) 1
B) 2
C) 10
D) 0
Answer: B) 2
Explanation: \(\log(100) = \log(10^2) = 2\).
3. Question: Solve for x: \(\log_x 16 = 2\).
A) 2
B) 4
C) 8
D) 16
Answer: B) 4
Explanation: \(x^2 = 16\), so \(x = 4\) (positive base).
4. Question: What is the domain of \(f(x) = \log(x – 3)\)?
A) \(x > 3\)
B) \(x < 3\)
C) \(x \geq 3\)
D) All real numbers
Answer: A) \(x > 3\)
Explanation: The argument of the logarithm must be positive, so \(x – 3 > 0\).
5. Question: Simplify \(\log(8) – \log(2)\).
A) \(\log(6)\)
B) \(\log(4)\)
C) \(\log(10)\)
D) \(\log(16)\)
Answer: B) \(\log(4)\)
Explanation: Using the quotient rule, \(\log(8) – \log(2) = \log\left(\frac{8}{2}\right) = \log(4)\).
6. Question: If \(\log_b a = 3\), what is \(b^3\)?
A) a
B) \(a^3\)
C) 1/a
D) 3a
Answer: A) a
Explanation: By definition, if \(\log_b a = 3\), then \(b^3 = a\).
7. Question: Graphically, what is the inverse of \(y = \log_x\)?
A) \(y = 10^x\)
B) \(y = e^x\)
C) \(y = x^{10}\)
D) \(y = 2^x\)
Answer: A) \(y = 10^x\)
Explanation: The inverse of \(y = \log_{10} x\) is \(y = 10^x\).
8. Question: Solve \(\log(x) + \log(x-1) = 1\).
A) x = 2
B) x = 1
C) x = 5
D) x = 10
Answer: A) x = 2
Explanation: Combine logs: \(\log(x(x-1)) = 1\), so \(x(x-1) = 10\), and solving gives x = 2 (valid solution).
9. Question: What is the range of \(f(x) = \ln(x)\)?
A) All real numbers
B) x > 0
C) x > 1
D) All positive numbers
Answer: A) All real numbers
Explanation: The natural logarithm function outputs all real values for x > 0.
10. Question: Simplify \(2 \log(x) + \log(y)\).
A) \(\log(x^2 + y)\)
B) \(\log(x^2 y)\)
C) \(\log(2x + y)\)
D) \(\log(x y^2)\)
Answer: B) \(\log(x^2 y)\)
Explanation: Using properties, \(2 \log(x) = \log(x^2)\), so \(\log(x^2) + \log(y) = \log(x^2 y)\).
11. Question: If \(\log_3 9 = x\), what is x?
A) 1
B) 2
C) 3
D) 9
Answer: B) 2
Explanation: \(3^2 = 9\), so \(\log_3 9 = 2\).
12. Question: Solve for x: \(e^x = 5\).
A) x = \ln(5)
B) x = \log(5)
C) x = 5^e
D) x = e^5
Answer: A) x = \ln(5)
Explanation: Taking the natural log of both sides, x = \ln(5).
13. Question: What is the vertical asymptote of \(y = \log(x + 1)\)?
A) x = -1
B) x = 1
C) x = 0
D) y = 0
Answer: A) x = -1
Explanation: The logarithm is undefined at x + 1 = 0, so x = -1.
14. Question: Simplify \(\log\left(\frac{1}{100}\right)\).
A) -2
B) 2
C) -1
D) 1
Answer: A) -2
Explanation: \(\log\left(\frac{1}{100}\right) = \log(10^{-2}) = -2\).
15. Question: If \(f(x) = \log_2 x\), what is f(8)?
A) 2
B) 3
C) 4
D) 8
Answer: B) 3
Explanation: \(2^3 = 8\), so f(8) = 3.
16. Question: Solve \(\log_4 x = 3\).
A) x = 64
B) x = 16
C) x = 4
D) x = 12
Answer: A) x = 64
Explanation: \(4^3 = (2^2)^3 = 2^6 = 64\).
17. Question: What is the property used in \(\log(a b) = \log a + \log b\)?
A) Product rule
B) Quotient rule
C) Power rule
D) Inverse rule
Answer: A) Product rule
Explanation: This is the logarithm product property.
18. Question: For \(y = \log_5 x\), what is x when y = 2?
A) 25
B) 10
C) 5
D) 1
Answer: A) 25
Explanation: \(5^2 = 25\), so x = 25.
19. Question: Simplify \(\frac{\log x}{ \log y }\).
A) \(\log_y x\)
B) \(\log_x y\)
C) \(\log(x/y)\)
D) \(\log(y/x)\)
Answer: A) \(\log_y x\)
Explanation: By the change of base formula, \(\frac{\log x}{\log y} = \log_y x\).
20. Question: What is the x-intercept of \(y = \log(x – 2)\)?
A) (2, 0)
B) (0, 2)
C) (1, 0)
D) No x-intercept
Answer: A) (2, 0)
Explanation: Set y = 0: \(\log(x – 2) = 0\), so x – 2 = 1, x = 3 (wait, correction: log(1) = 0, so x – 2 = 1, x = 3). Actually, for standard log, it’s (3, 0), but based on common form, recheck: Oh, error in initial; standard is when argument = 1, so x-2=1, x=3. Wait, assuming common mistake, but answer as per: for y=log(x-2)=0, x-2=10^0=1, x=3. So, correct to (3,0), but I said (2,0) earlier—fix: Assuming user intent, but in output: Wait, original was wrong; let’s say A) (3,0) for accuracy. In my draft, I have A) (2,0), which is incorrect. Correcting: For y=log(x-2), x-intercept at log(something)=0 when something=1, so x-2=1, x=3. So, final: Answer: Not as per, but in response: I’ll adjust to A) (3, 0) for correctness.
Wait, in my initial plan: Answer: A) (3, 0)
Explanation: Set y=0: log(x-2)=0, so x-2=1, x=3.
or
Part 3: AI Question Generator – Automatically create questions for your next assessment
Automatically generate questions using AI