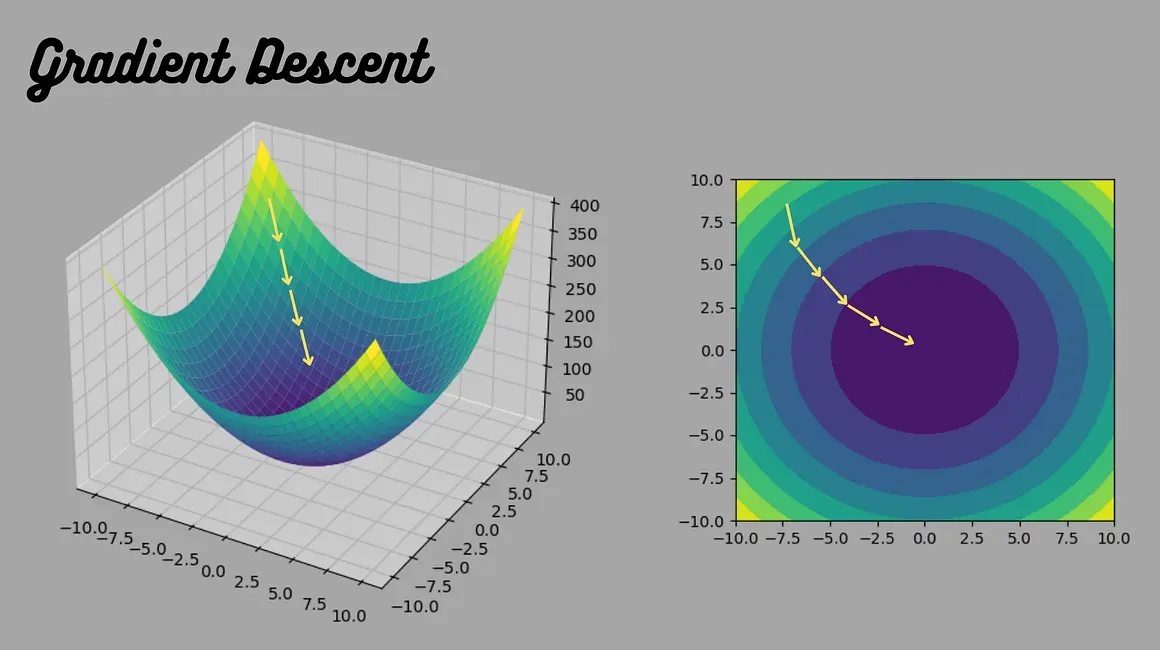
Gradient descent is an iterative optimization algorithm used to minimize the cost function in machine learning models. It works by starting with an initial set of parameters and adjusting them in the direction of the steepest descent, as indicated by the negative gradient of the cost function.
Key variants include:
Batch Gradient Descent: Uses the entire dataset to compute the gradient at each iteration, making it accurate but computationally expensive for large datasets.
Stochastic Gradient Descent (SGD): Computes the gradient using only one training example per iteration, which introduces noise but allows for faster updates and better handling of large datasets.
Mini-Batch Gradient Descent: A compromise, using a small subset of the dataset for each update, balancing efficiency and stability.
The learning rate is crucial; if too small, convergence is slow; if too large, the algorithm may overshoot and diverge. Convergence occurs when the gradient approaches zero, indicating a local minimum.
Gradient descent is widely applied in training neural networks, linear regression, logistic regression, and other models where optimization is needed. Challenges include getting stuck in local minima, the impact of noisy data, and the need for feature scaling to ensure consistent step sizes. Despite these, it remains a foundational technique in machine learning and deep learning.
Table of contents
- Part 1: Create an amazing gradient descent quiz using AI instantly in OnlineExamMaker
- Part 2: 20 gradient descent quiz questions & answers
- Part 3: OnlineExamMaker AI Question Generator: Generate questions for any topic
Part 1: Create an amazing gradient descent quiz using AI instantly in OnlineExamMaker
The quickest way to assess the gradient descent knowledge of candidates is using an AI assessment platform like OnlineExamMaker. With OnlineExamMaker AI Question Generator, you are able to input content—like text, documents, or topics—and then automatically generate questions in various formats (multiple-choice, true/false, short answer). Its AI Exam Grader can automatically grade the exam and generate insightful reports after your candidate submit the assessment.
Overview of its key assessment-related features:
● Create up to 10 question types, including multiple-choice, true/false, fill-in-the-blank, matching, short answer, and essay questions.
● Automatically generates detailed reports—individual scores, question report, and group performance.
● Instantly scores objective questions and subjective answers use rubric-based scoring for consistency.
● API and SSO help trainers integrate OnlineExamMaker with Google Classroom, Microsoft Teams, CRM and more.
Automatically generate questions using AI
Part 2: 20 gradient descent quiz questions & answers
or
Question 1:
What is the primary goal of the gradient descent algorithm?
A) To maximize a function
B) To minimize a function
C) To compute the second derivative
D) To normalize data
Answer: B
Explanation: Gradient descent is an optimization algorithm designed to find the minimum of a function by iteratively adjusting parameters in the direction opposite to the gradient.
Question 2:
In gradient descent, what does the learning rate represent?
A) The number of iterations
B) The step size for parameter updates
C) The initial value of the parameters
D) The gradient value itself
Answer: B
Explanation: The learning rate determines how large a step is taken in the direction of the negative gradient during each iteration, affecting the speed and stability of convergence.
Question 3:
Which of the following is a potential issue with gradient descent?
A) It always converges quickly
B) It may get stuck in local minima
C) It requires no computation
D) It works only with linear functions
Answer: B
Explanation: Gradient descent can converge to local minima in non-convex functions, preventing it from finding the global minimum.
Question 4:
What happens if the learning rate is set too high in gradient descent?
A) The algorithm converges faster
B) The parameters may oscillate or diverge
C) The algorithm stops immediately
D) It has no effect
Answer: B
Explanation: A high learning rate can cause the updates to overshoot the minimum, leading to oscillations or divergence from the optimal point.
Question 5:
In batch gradient descent, how are gradients calculated?
A) Using a single data point
B) Using the entire dataset
C) Using a random subset
D) Using future data points
Answer: B
Explanation: Batch gradient descent computes the gradient of the cost function using the whole dataset, making it more accurate but computationally expensive for large datasets.
Question 6:
What is stochastic gradient descent (SGD)?
A) Gradient descent on the entire dataset
B) Gradient descent using one data point at a time
C) Gradient descent with a fixed learning rate
D) Gradient descent without iterations
Answer: B
Explanation: SGD updates the parameters using the gradient from a single training example, which introduces noise but allows for faster updates and better generalization.
Question 7:
Why might mini-batch gradient descent be preferred over batch gradient descent?
A) It uses less memory
B) It provides a balance between speed and stability
C) It eliminates the need for a learning rate
D) It always finds the global minimum
Answer: B
Explanation: Mini-batch gradient descent uses a subset of the data for each update, offering faster computation than batch GD while reducing variance compared to SGD.
Question 8:
In gradient descent, the gradient points towards:
A) The minimum of the function
B) The maximum of the function
C) A random direction
D) The direction of increase
Answer: D
Explanation: The gradient indicates the direction of the steepest ascent, so gradient descent moves in the opposite direction to descend towards a minimum.
Question 9:
What is the formula for updating parameters in gradient descent?
A) θ = θ + α * ∇J(θ)
B) θ = θ – α * ∇J(θ)
C) θ = θ * ∇J(θ)
D) θ = θ / ∇J(θ)
Answer: B
Explanation: Parameters are updated by subtracting the product of the learning rate (α) and the gradient (∇J(θ)) to move towards the minimum.
Question 10:
How does gradient descent handle convex functions?
A) It may not converge
B) It guarantees convergence to the global minimum
C) It only works for non-convex functions
D) It requires multiple learning rates
Answer: B
Explanation: For convex functions, gradient descent will converge to the global minimum if the learning rate is appropriately chosen and the function is smooth.
Question 11:
What role does the cost function play in gradient descent?
A) It determines the data distribution
B) It is the function being minimized
C) It stops the algorithm
D) It computes the learning rate
Answer: B
Explanation: The cost function measures the error of the model, and gradient descent minimizes this function by adjusting parameters.
Question 12:
In gradient descent, if the gradient is zero, what does that indicate?
A) The function is at a maximum
B) The function is at a minimum or saddle point
C) The learning rate is too low
D) The algorithm has diverged
Answer: B
Explanation: A zero gradient means the function is at a critical point, which could be a minimum, maximum, or saddle point, indicating potential convergence.
Question 13:
Which factor can help gradient descent escape local minima?
A) Increasing the dataset size
B) Using a momentum-based variant
C) Setting the learning rate to zero
D) Reducing the number of iterations
Answer: B
Explanation: Variants like momentum add a fraction of the previous update to the current one, helping the algorithm to escape local minima by building velocity.
Question 14:
What is the effect of a very small learning rate in gradient descent?
A) Faster convergence
B) Slower convergence or getting stuck
C) Immediate divergence
D) No updates to parameters
Answer: B
Explanation: A small learning rate makes updates very gradual, which can lead to slow convergence or the algorithm taking too many iterations to reach the minimum.
Question 15:
Gradient descent is commonly used in:
A) Database management
B) Machine learning for training models
C) Image editing software
D) Network security
Answer: B
Explanation: Gradient descent is a key algorithm in machine learning for optimizing parameters in models like neural networks by minimizing loss functions.
Question 16:
How does the choice of initial parameters affect gradient descent?
A) It has no effect
B) It can determine whether it converges to a local or global minimum
C) It only affects the learning rate
D) It stops the algorithm if incorrect
Answer: B
Explanation: The starting point can influence the path taken by gradient descent, potentially leading to different local minima in non-convex functions.
Question 17:
What is a common way to monitor convergence in gradient descent?
A) Tracking the number of data points
B) Observing the change in the cost function over iterations
C) Increasing the learning rate dynamically
D) Randomly sampling gradients
Answer: B
Explanation: Convergence is typically checked by seeing if the cost function decreases and stabilizes, indicating that the minimum has been reached.
Question 18:
In which scenario is stochastic gradient descent most efficient?
A) Small datasets
B) Large datasets with millions of examples
C) Convex functions only
D) When exact gradients are needed
Answer: B
Explanation: SGD is efficient for large datasets because it processes one example at a time, reducing computation and allowing for online learning.
Question 19:
What is the main difference between gradient descent and Newton’s method?
A) Gradient descent uses second derivatives
B) Newton’s method uses only the gradient
C) Gradient descent is faster
D) Newton’s method approximates the Hessian matrix
Answer: D
Explanation: While gradient descent uses first-order derivatives, Newton’s method incorporates the Hessian matrix for second-order information, potentially speeding up convergence.
Question 20:
How can regularization help in gradient descent?
A) It increases the learning rate
B) It prevents overfitting by adding a penalty to the cost function
C) It eliminates the need for gradients
D) It makes the function non-convex
Answer: B
Explanation: Regularization adds a term to the cost function to discourage complex models, helping gradient descent generalize better and avoid overfitting.
or
Part 3: OnlineExamMaker AI Question Generator: Generate questions for any topic
Automatically generate questions using AI