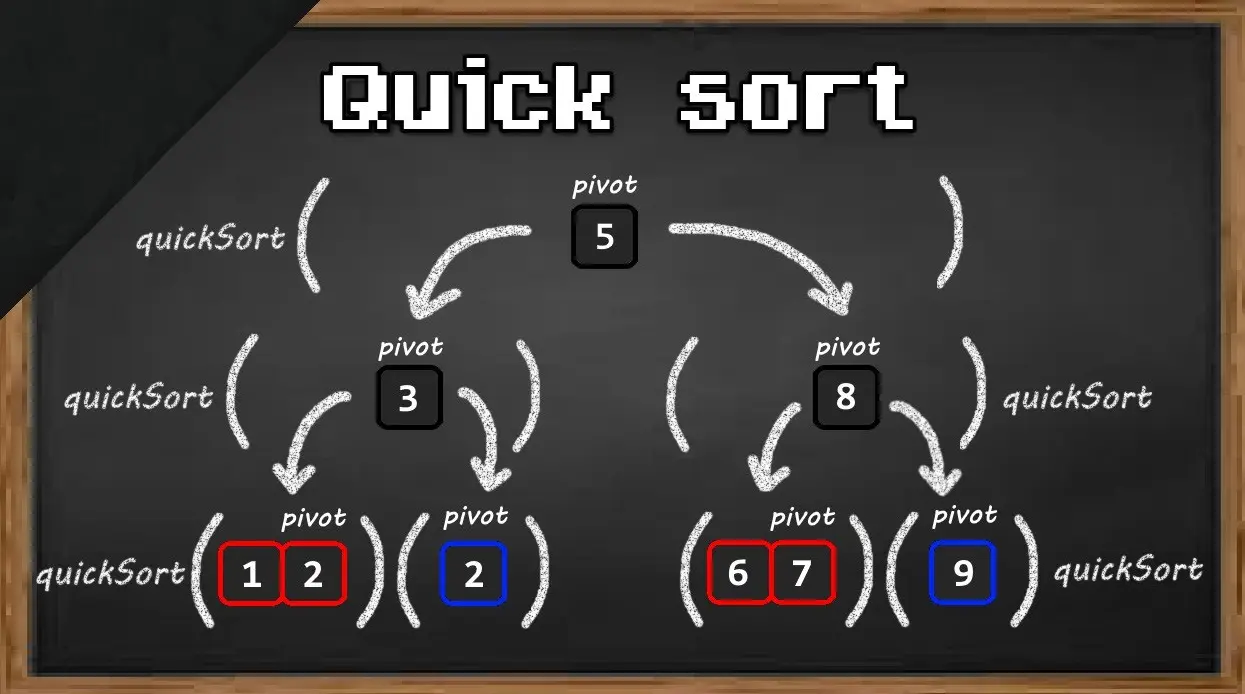
Quick Sort is a highly efficient divide-and-conquer sorting algorithm that works by selecting a ‘pivot’ element from an array and partitioning the other elements into two sub-arrays: one with elements less than the pivot and another with elements greater than the pivot. The sub-arrays are then sorted recursively until the entire array is sorted.
Here’s a step-by-step overview:
1. Choose a pivot: Select an element from the array, often the last element, first element, or a random one.
2. Partition the array: Rearrange the elements so that all elements less than the pivot come before it, and all elements greater come after it. The pivot ends up in its final sorted position.
3. Recur: Apply the above steps recursively to the sub-arrays formed on either side of the pivot until the base case is reached (sub-arrays of size 0 or 1).
Quick Sort is favored for its average time complexity of O(n log n), making it faster than many other sorting algorithms in practice, though its worst-case complexity is O(n²) if the pivot is chosen poorly. It’s widely used in programming languages like C++’s std::sort due to its efficiency and in-place sorting capability, which minimizes space usage.
Table of Contents
- Part 1: Create A Quick Sort Quiz in Minutes Using AI with OnlineExamMaker
- Part 2: 20 Quick Sort Quiz Questions & Answers
- Part 3: AI Question Generator – Automatically Create Questions for Your Next Assessment
Part 1: Create A Quick Sort Quiz in Minutes Using AI with OnlineExamMaker
When it comes to ease of creating a Quick Sort skills assessment, OnlineExamMaker is one of the best AI-powered quiz making software for your institutions or businesses. With its AI Question Generator, just upload a document or input keywords about your assessment topic, you can generate high-quality quiz questions on any topic, difficulty level, and format.
Overview of its key assessment-related features:
● AI Question Generator to help you save time in creating quiz questions automatically.
● Share your online exam with audiences on social platforms like Facebook, Twitter, Reddit and more.
● Instantly scores objective questions and subjective answers use rubric-based scoring for consistency.
● Simply copy and insert a few lines of embed codes to display your online exams on your website or WordPress blog.
Automatically generate questions using AI
Part 2: 20 Quick Sort Quiz Questions & Answers
or
Question 1:
What is Quick Sort?
A) A comparison-based sorting algorithm that uses divide-and-conquer
B) A sorting algorithm that uses extra space for merging
C) A linear time sorting algorithm
D) A sorting algorithm that only works on linked lists
Answer: A
Explanation: Quick Sort is a comparison-based sorting algorithm that follows the divide-and-conquer strategy by selecting a pivot and partitioning the array.
Question 2:
In Quick Sort, what is the role of the pivot element?
A) It divides the array into two halves
B) It is the smallest element in the array
C) It is swapped with the last element
D) It determines the array’s size
Answer: A
Explanation: The pivot element is used to partition the array such that elements less than the pivot are on one side and greater elements are on the other, dividing the array for recursive sorting.
Question 3:
Which of the following is a common method for selecting a pivot in Quick Sort?
A) Always choose the middle element
B) Always choose the first element
C) Randomly select an element
D) All of the above
Answer: D
Explanation: Pivot selection can vary; common methods include choosing the first element, last element, middle element, or a random element to help avoid worst-case scenarios.
Question 4:
What is the best-case time complexity of Quick Sort?
A) O(n)
B) O(n log n)
C) O(n^2)
D) O(1)
Answer: A
Explanation: The best-case time complexity occurs when the pivot divides the array into two equal parts each time, resulting in O(n) time, though this is rare.
Question 5:
What is the average-case time complexity of Quick Sort?
A) O(n)
B) O(n log n)
C) O(n^2)
D) O(log n)
Answer: B
Explanation: On average, Quick Sort performs at O(n log n) due to the balanced partitions created by the pivot, making it efficient for most datasets.
Question 6:
What is the worst-case time complexity of Quick Sort?
A) O(n)
B) O(n log n)
C) O(n^2)
D) O(n + k)
Answer: C
Explanation: The worst-case occurs when the pivot is the smallest or largest element, leading to unbalanced partitions and O(n^2) time complexity, such as with a sorted array.
Question 7:
How can the worst-case scenario of Quick Sort be avoided?
A) By always choosing the median as pivot
B) By using random pivot selection
C) By sorting the array first
D) By increasing array size
Answer: B
Explanation: Random pivot selection helps avoid worst-case partitions by making it unlikely for the pivot to consistently create unbalanced splits.
Question 8:
Is Quick Sort an in-place sorting algorithm?
A) Yes
B) No
C) Only for small arrays
D) Only for large arrays
Answer: A
Explanation: Quick Sort is an in-place algorithm because it sorts the array without requiring additional storage proportional to the input size, using only a constant amount of extra space.
Question 9:
What is the space complexity of Quick Sort?
A) O(1)
B) O(n)
C) O(log n)
D) O(n log n)
Answer: C
Explanation: Quick Sort uses O(log n) space on average due to the recursion stack for the divide-and-conquer calls, though it can reach O(n) in the worst case.
Question 10:
Is Quick Sort a stable sorting algorithm?
A) Yes
B) No
C) It depends on the implementation
D) Only for even-sized arrays
Answer: B
Explanation: Quick Sort is not stable because elements with equal keys may change their relative order during the partitioning process.
Question 11:
In Quick Sort, after partitioning, what happens to the subarrays?
A) They are sorted recursively
B) They are merged together
C) They are discarded
D) They are reversed
Answer: A
Explanation: After partitioning, the subarrays on either side of the pivot are sorted recursively using the same Quick Sort process until the entire array is sorted.
Question 12:
Which pivot selection strategy is likely to give the best performance?
A) Always the first element
B) Median of three elements
C) Always the last element
D) Random element
Answer: B
Explanation: Selecting the median of three elements (e.g., first, middle, last) as the pivot often leads to more balanced partitions, improving average performance.
Question 13:
How does Quick Sort handle an already sorted array?
A) It performs efficiently
B) It takes O(n log n) time
C) It may take O(n^2) time if worst pivot is chosen
D) It crashes the program
Answer: C
Explanation: If the pivot is chosen as the first or last element in a sorted array, it leads to worst-case O(n^2) time complexity due to unbalanced partitions.
Question 14:
What is the primary advantage of Quick Sort over Merge Sort?
A) It is stable
B) It uses less space
C) It is always faster
D) It works only on arrays
Answer: B
Explanation: Quick Sort is an in-place algorithm with O(log n) space complexity, whereas Merge Sort requires O(n) extra space for merging.
Question 15:
In Quick Sort, what does the partition function do?
A) Swaps elements to place the pivot in its final position
B) Sorts the entire array
C) Removes duplicates
D) Reverses the array
Answer: A
Explanation: The partition function rearranges the array so that all elements less than the pivot are on the left, and all greater are on the right, placing the pivot in its sorted position.
Question 16:
Can Quick Sort be used for linked lists?
A) Yes, with modifications
B) No, only for arrays
C) Yes, without changes
D) Only for circular linked lists
Answer: A
Explanation: Quick Sort can be adapted for linked lists, but it requires changes to the partitioning process since random access is not available as in arrays.
Question 17:
What happens if all elements in the array are the same in Quick Sort?
A) It works efficiently
B) It may lead to O(n^2) time
C) It stops immediately
D) It requires a different algorithm
Answer: B
Explanation: If all elements are identical and a poor pivot is chosen, it can result in unbalanced partitions, leading to worst-case O(n^2) time complexity.
Question 18:
Which of the following is true about Quick Sort’s recursion?
A) It is tail-recursive
B) It uses iteration instead
C) It can cause stack overflow for large arrays
D) It is not recursive
Answer: C
Explanation: Quick Sort’s recursive calls can lead to stack overflow for very large arrays in the worst case, as the recursion depth can reach O(n).
Question 19:
Why is Quick Sort often preferred in practice despite its worst-case complexity?
A) It has a small constant factor in O(n log n)
B) It is always stable
C) It uses no comparisons
D) It requires no pivot
Answer: A
Explanation: Quick Sort’s average performance is excellent with a low constant factor, making it faster in practice for most real-world datasets compared to its theoretical worst case.
Question 20:
In which scenario would Quick Sort perform poorly?
A) Randomly ordered arrays
B) Nearly sorted arrays with poor pivot choice
C) Arrays with duplicates
D) Small arrays
Answer: B
Explanation: Quick Sort performs poorly on nearly sorted arrays if the pivot selection leads to unbalanced partitions, resulting in O(n^2) time complexity.
or
Part 3: AI Question Generator – Automatically Create Questions for Your Next Assessment
Automatically generate questions using AI