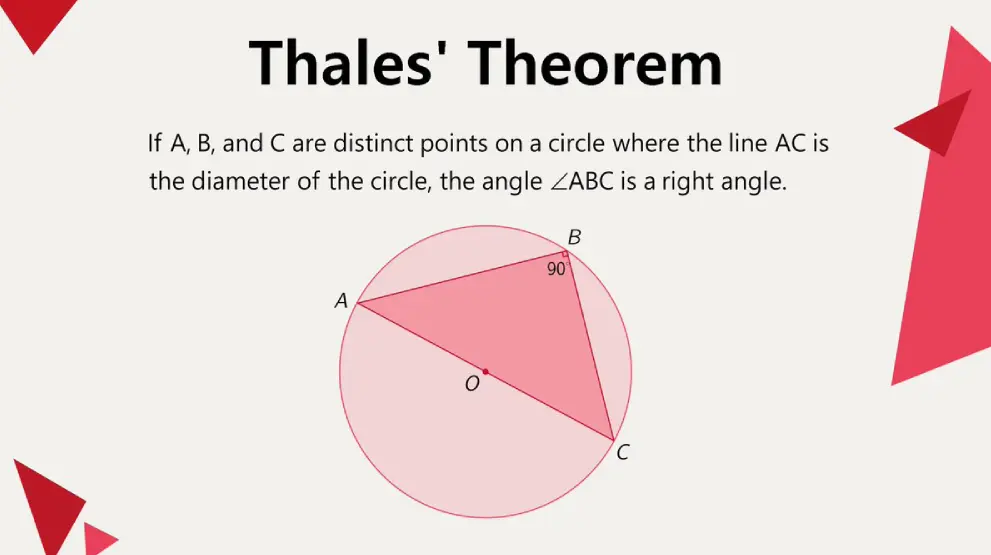
Thales’ Theorem, attributed to the ancient Greek mathematician Thales of Miletus, states that if A and C are the endpoints of a diameter of a circle, and B is any point on the circle distinct from A and C, then the angle at B in triangle ABC is a right angle (90 degrees). This means that any triangle inscribed in a semicircle with the diameter as one side will have a right-angled vertex at the point on the circumference. The theorem is a foundational principle in Euclidean geometry, illustrating the properties of circles and right triangles.
Table of Contents
- Part 1: Create A Thales’S Theorem Quiz in Minutes Using AI with OnlineExamMaker
- Part 2: 20 Thales’S Theorem Quiz Questions & Answers
- Part 3: AI Question Generator – Automatically Create Questions for Your Next Assessment
Part 1: Create A Thales’S Theorem Quiz in Minutes Using AI with OnlineExamMaker
Are you looking for an online assessment to test the Thales’S Theorem skills of your learners? OnlineExamMaker uses artificial intelligence to help quiz organizers to create, manage, and analyze exams or tests automatically. Apart from AI features, OnlineExamMaker advanced security features such as full-screen lockdown browser, online webcam proctoring, and face ID recognition.
Recommended features for you:
● Includes a safe exam browser (lockdown mode), webcam and screen recording, live monitoring, and chat oversight to prevent cheating.
● Enhances assessments with interactive experience by embedding video, audio, image into quizzes and multimedia feedback.
● Once the exam ends, the exam scores, question reports, ranking and other analytics data can be exported to your device in Excel file format.
● Offers question analysis to evaluate question performance and reliability, helping instructors optimize their training plan.
Automatically generate questions using AI
Part 2: 20 Thales’S Theorem Quiz Questions & Answers
or
1. Question: In a circle with diameter AC, point B lies on the circumference. What is the measure of angle ABC?
Options: A. 90 degrees
B. 180 degrees
C. 60 degrees
D. 120 degrees
Answer: A
Explanation: Thales’ Theorem states that the angle subtended by a diameter at any point on the circle is a right angle, so angle ABC is 90 degrees.
2. Question: If a triangle is inscribed in a semicircle with one side as the diameter, what type of triangle is it?
Options: A. Right-angled
B. Isosceles
C. Equilateral
D. Scalene
Answer: A
Explanation: According to Thales’ Theorem, the angle opposite the diameter is 90 degrees, making the triangle right-angled.
3. Question: In a circle, points A, B, and C are on the circumference with AC as the diameter. What is true about angle at B?
Options: A. It is 90 degrees
B. It is greater than 90 degrees
C. It is less than 90 degrees
D. It varies based on the circle’s radius
Answer: A
Explanation: Thales’ Theorem guarantees that the angle at B, subtended by the diameter AC, is always 90 degrees.
4. Question: For Thales’ Theorem to hold, which of the following must be true?
Options: A. The line segment is the diameter
B. The points are on the circumference
C. Both A and B
D. Neither A nor B
Answer: C
Explanation: Thales’ Theorem requires that the line segment be the diameter and the third point be on the circumference for the angle to be 90 degrees.
5. Question: If angle ABC is 90 degrees and points A, B, C are on a circle, what must AC be?
Options: A. The diameter
B. A chord
C. A radius
D. A tangent
Answer: A
Explanation: The converse of Thales’ Theorem states that if an angle subtended by a chord is 90 degrees, that chord must be the diameter.
6. Question: In a circle of radius 5 cm, diameter AB is drawn, and point C is on the circumference. What is the measure of angle ACB?
Options: A. 90 degrees
B. 45 degrees
C. 30 degrees
D. 60 degrees
Answer: A
Explanation: Thales’ Theorem applies regardless of the radius; the angle at C subtended by diameter AB is 90 degrees.
7. Question: Which theorem explains why a triangle with one side as the diameter of a circle and the opposite vertex on the circumference is right-angled?
Options: A. Thales’ Theorem
B. Pythagoras’ Theorem
C. Euclid’s Theorem
D. Pascal’s Theorem
Answer: A
Explanation: Thales’ Theorem directly states this property for triangles inscribed in a semicircle.
8. Question: If AB is the diameter of a circle and C is a point on the circle, what is the relationship between triangle ABC and a right angle?
Options: A. Angle at C is 90 degrees
B. Angle at A is 90 degrees
C. Angle at B is 90 degrees
D. No angle is 90 degrees
Answer: A
Explanation: Thales’ Theorem specifies that the angle at the point on the circumference (C) is 90 degrees.
9. Question: Can Thales’ Theorem be applied if the point is inside the circle instead of on the circumference?
Options: A. No
B. Yes
C. Only if it’s the center
D. Only if it’s on a radius
Answer: A
Explanation: Thales’ Theorem requires the third point to be on the circumference; inside points do not form a 90-degree angle with the diameter.
10. Question: In a circle, if AC is not the diameter but a chord, and B is on the circumference, what is angle ABC?
Options: A. Not necessarily 90 degrees
B. Always 90 degrees
C. 180 degrees
D. 0 degrees
Answer: A
Explanation: Thales’ Theorem only applies when the chord is the diameter; otherwise, the angle at B is not guaranteed to be 90 degrees.
11. Question: What is the key condition for Thales’ Theorem?
Options: A. A straight line as diameter
B. An equilateral triangle
C. Parallel lines
D. Congruent triangles
Answer: A
Explanation: The theorem hinges on having a diameter as the base, with the third point on the circle, resulting in a right angle.
12. Question: If a right-angled triangle has its hypotenuse as the diameter of a circle, where must the right-angled vertex be?
Options: A. On the circumference
B. At the center
C. Outside the circle
D. On the diameter
Answer: A
Explanation: Thales’ Theorem confirms that for the hypotenuse to be the diameter, the right-angled vertex must lie on the circumference.
13. Question: In Thales’ Theorem, if the circle’s diameter is 10 units, and points A and C are the endpoints, what is angle at B on the circumference?
Options: A. 90 degrees
B. 45 degrees
C. Depends on B’s position
D. 180 degrees
Answer: A
Explanation: The length of the diameter does not affect the angle; Thales’ Theorem always gives 90 degrees at B.
14. Question: Which of the following is a direct application of Thales’ Theorem?
Options: A. Proving a right angle in a semicircle
B. Calculating the area of a circle
C. Finding the circumference
D. Drawing tangents
Answer: A
Explanation: Thales’ Theorem is specifically used to demonstrate that an angle in a semicircle is a right angle.
15. Question: If two points form the diameter and a third point is on the circle, what shape is formed with these three points?
Options: A. A right-angled triangle
B. An acute triangle
C. An obtuse triangle
D. A square
Answer: A
Explanation: Thales’ Theorem ensures the triangle is right-angled at the third point.
16. Question: Does Thales’ Theorem work for circles of any size?
Options: A. Yes
B. No, only for large circles
C. No, only for small circles
D. Only for perfect circles
Answer: A
Explanation: The theorem is universal and applies to all circles, as long as the conditions of diameter and circumference point are met.
17. Question: In a circle, if angle at B is 90 degrees and A and C are fixed, what must AC be?
Options: A. The diameter
B. A radius
C. A tangent line
D. An arc
Answer: A
Explanation: The converse of Thales’ Theorem states that the side opposite the right angle must be the diameter.
18. Question: How many right angles are guaranteed in a triangle formed by Thales’ Theorem?
Options: A. One
B. Two
C. Three
D. None
Answer: A
Explanation: Thales’ Theorem guarantees exactly one right angle at the point on the circumference.
19. Question: If you extend Thales’ Theorem, what happens if the point is on the other side of the diameter?
Options: A. Still 90 degrees
B. Angle changes
C. No triangle forms
D. Angle is 180 degrees
Answer: A
Explanation: As long as the point is on the circumference and AC is the diameter, the angle remains 90 degrees regardless of the side.
20. Question: What is the primary geometric shape involved in Thales’ Theorem?
Options: A. Circle
B. Square
C. Rectangle
D. Triangle only
Answer: A
Explanation: Thales’ Theorem is based on properties of a circle, specifically with a diameter and a point on the circumference forming a right-angled triangle.
or
Part 3: AI Question Generator – Automatically Create Questions for Your Next Assessment
Automatically generate questions using AI