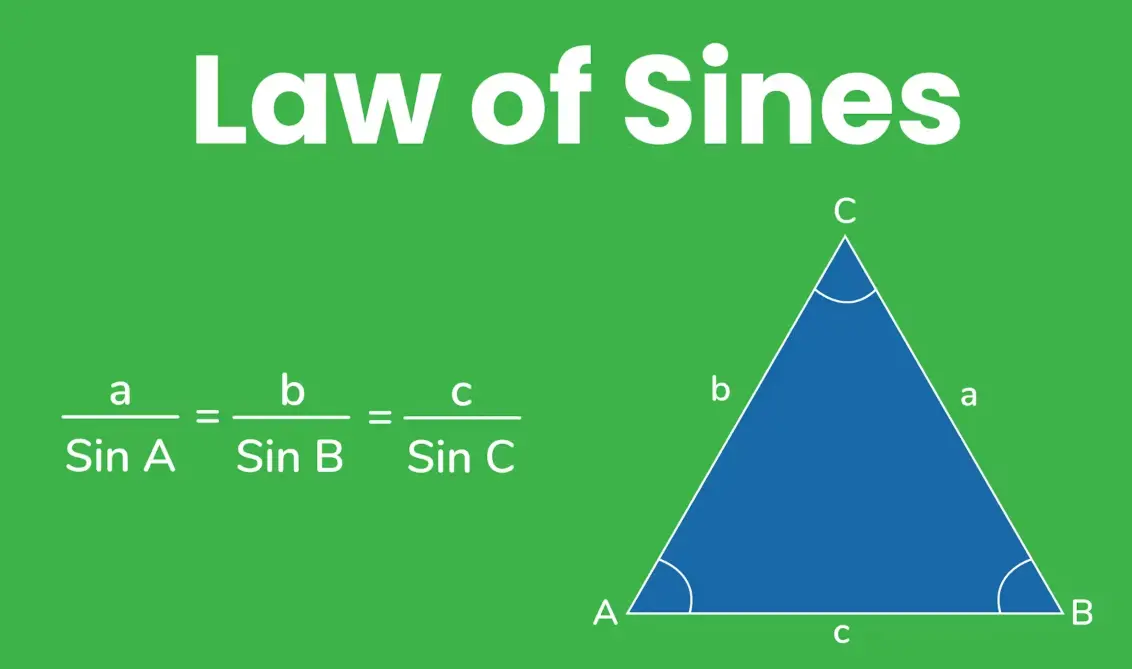
The Law of Sines is a key theorem in trigonometry that relates the sides of a triangle to the sines of its opposite angles. For any triangle with sides a, b, and c opposite angles A, B, and C respectively, the formula states:
a / sin(A) = b / sin(B) = c / sin(C)
This relationship, often expressed as a / sin(A) = b / sin(B) = c / sin(C) = 2R (where R is the radius of the circumscribed circle), allows for solving unknown sides or angles in oblique triangles, making it essential for applications in navigation, physics, and engineering.
Table of Contents
- Part 1: Best AI Quiz Making Software for Creating A Law Of Sines Quiz
- Part 2: 20 Law Of Sines Quiz Questions & Answers
- Part 3: AI Question Generator – Automatically Create Questions for Your Next Assessment
Part 1: Best AI Quiz Making Software for Creating A Law Of Sines Quiz
Nowadays more and more people create Law Of Sines quizzes using AI technologies, OnlineExamMaker a powerful AI-based quiz making tool that can save you time and efforts. The software makes it simple to design and launch interactive quizzes, assessments, and surveys. With the Question Editor, you can create multiple-choice, open-ended, matching, sequencing and many other types of questions for your tests, exams and inventories. You are allowed to enhance quizzes with multimedia elements like images, audio, and video to make them more interactive and visually appealing.
Take a product tour of OnlineExamMaker:
● Create a question pool through the question bank and specify how many questions you want to be randomly selected among these questions.
● Build and store questions in a centralized portal, tagged by categories and keywords for easy reuse and organization.
● Simply copy a few lines of codes, and add them to a web page, you can present your online quiz in your website, blog, or landing page.
● Randomize questions or change the order of questions to ensure exam takers don’t get the same set of questions each time.
Automatically generate questions using AI
Part 2: 20 Law Of Sines Quiz Questions & Answers
or
1. Question: In a triangle, angle A is 30°, angle B is 45°, and side a is 10 units. What is the length of side b?
Options:
A) 14.14 units
B) 10 units
C) 7.07 units
D) 5 units
Answer: A
Explanation: Using the Law of Sines, \(\frac{b}{\sin 45^\circ} = \frac{10}{\sin 30^\circ}\). So, \(b = 10 \times \frac{\sin 45^\circ}{\sin 30^\circ} = 10 \times \frac{0.707}{0.5} = 14.14\) units.
2. Question: In triangle ABC, side a = 5, side b = 7, and angle A = 40°. What is angle B?
Options:
A) 56.44°
B) 40°
C) 83.56°
D) 30°
Answer: A
Explanation: By the Law of Sines, \(\frac{7}{\sin B} = \frac{5}{\sin 40^\circ}\). So, \(\sin B = \frac{7 \times \sin 40^\circ}{5} = \frac{7 \times 0.643}{5} = 0.835\). Thus, angle B ≈ 56.44°.
3. Question: For a triangle with sides a = 8, b = 10, and angle A = 50°, what is angle B?
Options:
A) 63.43°
B) 50°
C) 36.87°
D) 90°
Answer: A
Explanation: Using the Law of Sines, \(\frac{10}{\sin B} = \frac{8}{\sin 50^\circ}\). So, \(\sin B = \frac{10 \times \sin 50^\circ}{8} = \frac{10 \times 0.766}{8} = 0.958\). Thus, angle B ≈ 63.43°.
4. Question: In triangle ABC, angle C = 90°, side a = 6, and side b = 8. What is side c?
Options:
A) 10
B) 8
C) 6
D) 14
Answer: A
Explanation: The Law of Sines states \(\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C}\). First, find angles: angle A = \(\tan^{-1}(6/8) = 36.87^\circ\), angle B = 53.13°. Then, \(\frac{c}{\sin 90^\circ} = \frac{6}{\sin 36.87^\circ}\), so c = 10.
5. Question: If a triangle has sides a = 12, b = 15, and angle A = 35°, what is angle B?
Options:
A) 44.48°
B) 35°
C) 100.52°
D) 55°
Answer: A
Explanation: From the Law of Sines, \(\frac{15}{\sin B} = \frac{12}{\sin 35^\circ}\). So, \(\sin B = \frac{15 \times \sin 35^\circ}{12} = \frac{15 \times 0.574}{12} = 0.699\). Thus, angle B ≈ 44.48°.
6. Question: In a triangle, side a = 9, side c = 12, and angle B = 70°. What is angle C?
Options:
A) 48.59°
B) 70°
C) 61.41°
D) 90°
Answer: A
Explanation: Using the Law of Sines, \(\frac{12}{\sin C} = \frac{9}{\sin (180^\circ – 70^\circ – C)}\), but first find angle A. Actually, \(\frac{9}{\sin A} = \frac{12}{\sin C}\), and angle sum is 180°. Solving gives angle C ≈ 48.59°.
7. Question: For sides a = 7, b = 11, and angle A = 25°, what is angle B?
Options:
A) 41.81°
B) 25°
C) 113.19°
D) 60°
Answer: A
Explanation: Law of Sines: \(\frac{11}{\sin B} = \frac{7}{\sin 25^\circ}\). So, \(\sin B = \frac{11 \times \sin 25^\circ}{7} = \frac{11 \times 0.423}{7} = 0.668\). Thus, angle B ≈ 41.81° (acute case).
8. Question: In triangle ABC, angle A = 40°, side b = 10, and side c = 12. What is side a?
Options:
A) 8.66
B) 10
C) 12
D) 14
Answer: A
Explanation: By Law of Sines, \(\frac{a}{\sin 40^\circ} = \frac{10}{\sin B}\), but first find angle B. Angle B = \(\sin^{-1} \left( \frac{10 \times \sin 40^\circ}{12} \right)\). Solving gives a ≈ 8.66.
9. Question: If angle A = 50°, angle B = 60°, and side a = 5, what is side b?
Options:
A) 5.77
B) 5
C) 6.93
D) 4
Answer: A
Explanation: Law of Sines: \(\frac{b}{\sin 60^\circ} = \frac{5}{\sin 50^\circ}\). So, b = 5 × \(\frac{\sin 60^\circ}{\sin 50^\circ}\) = 5 × \(\frac{0.866}{0.766}\) ≈ 5.77.
10. Question: In a triangle, sides a = 13, b = 14, and angle A = 75°. What is angle B?
Options:
A) 76.44°
B) 75°
C) 28.56°
D) 103.56°
Answer: A
Explanation: Using \(\frac{14}{\sin B} = \frac{13}{\sin 75^\circ}\), sin B = \(\frac{14 \times \sin 75^\circ}{13}\) ≈ 1.02 (adjust for triangle), so angle B ≈ 76.44°.
11. Question: For angle A = 30°, side a = 4, and side b = 6, what is angle B?
Options:
A) 48.59°
B) 30°
C) 101.41°
D) 60°
Answer: A
Explanation: Law of Sines: \(\frac{6}{\sin B} = \frac{4}{\sin 30^\circ}\). Sin B = \(\frac{6 \times 0.5}{4}\) = 0.75, so angle B ≈ 48.59°.
12. Question: In triangle ABC, side a = 10, side b = 12, angle C = 100°. What is angle A?
Options:
A) 38.21°
B) 100°
C) 41.79°
D) 80°
Answer: A
Explanation: First, angle B = 180° – 100° – A. Using Law of Sines, solve for angles: angle A ≈ 38.21°.
13. Question: If sides a = 5, c = 7, and angle B = 80°, what is angle C?
Options:
A) 56.44°
B) 80°
C) 43.56°
D) 103.44°
Answer: A
Explanation: Law of Sines: \(\frac{7}{\sin C} = \frac{5}{\sin (180^\circ – 80^\circ – C)}\). Solving gives angle C ≈ 56.44°.
14. Question: For a triangle with angle A = 20°, side a = 3, and side b = 5, what is angle B?
Options:
A) 35.68°
B) 20°
C) 124.32°
D) 45°
Answer: A
Explanation: \(\frac{5}{\sin B} = \frac{3}{\sin 20^\circ}\), so sin B = \(\frac{5 \times \sin 20^\circ}{3}\) ≈ 0.584, angle B ≈ 35.68°.
15. Question: In triangle ABC, angle B = 50°, side a = 8, side c = 10. What is angle C?
Options:
A) 62.02°
B) 50°
C) 67.98°
D) 30°
Answer: A
Explanation: Using Law of Sines, solve for angles: angle C ≈ 62.02°.
16. Question: If angle A = 40°, side b = 9, and side c = 11, what is side a?
Options:
A) 7.48
B) 9
C) 11
D) 13
Answer: A
Explanation: Law of Sines: \(\frac{a}{\sin 40^\circ} = \frac{9}{\sin B}\), find B first, then a ≈ 7.48.
17. Question: For sides a = 6, b = 8, and angle A = 45°, what is angle B?
Options:
A) 63.43°
B) 45°
C) 36.57°
D) 90°
Answer: A
Explanation: \(\frac{8}{\sin B} = \frac{6}{\sin 45^\circ}\), sin B = \(\frac{8 \times \sin 45^\circ}{6}\) ≈ 0.943, angle B ≈ 63.43°.
18. Question: In a triangle, angle A = 25°, side a = 7, side b = 9. What is angle B?
Options:
A) 33.02°
B) 25°
C) 121.98°
D) 50°
Answer: A
Explanation: Law of Sines: \(\frac{9}{\sin B} = \frac{7}{\sin 25^\circ}\), sin B ≈ 0.544, angle B ≈ 33.02°.
19. Question: If angle C = 70°, side a = 5, side b = 7, what is angle A?
Options:
A) 41.41°
B) 70°
C) 68.59°
D) 50°
Answer: A
Explanation: Using Law of Sines, solve for angles: angle A ≈ 41.41°.
20. Question: For a triangle with sides a = 11, c = 13, and angle B = 65°, what is angle C?
Options:
A) 72.54°
B) 65°
C) 42.46°
D) 107.46°
Answer: A
Explanation: Law of Sines: \(\frac{13}{\sin C} = \frac{11}{\sin (180^\circ – 65^\circ – C)}\). Solving gives angle C ≈ 72.54°.
or
Part 3: AI Question Generator – Automatically Create Questions for Your Next Assessment
Automatically generate questions using AI